Menu

Production Function

The production function expresses a functional relationship between physical inputs and physical outputs of a firm at any particular time period. The output is thus a function of inputs. So, production function is an input – output relationship. Mathematically production function can be written as:

Q = f(L1, L2, C, O, T)

Let’s denote:

  • Q: Output
  • f: Function of L1 (Land)
  • L2: Labour
  • C: Capital
  • O: Organization
  • T: Technology

Here output is the function of inputs. Hence output becomes the dependent variable and inputs are the independent variables.

Definition:

Samuelson defines the production function as “The technical relationship which reveals the maximum amount of output capable of being produced by each and every set of inputs.”

Michael R Baye defines the production function as “That function which defines the maximum amount of output that can be produced with a given set of inputs.”

Assumptions:

Production function has the following assumptions:

  1. The production function is related to a particular period of time.
  2. There is no change in technology.
  3. The producer is using the best techniques available.
  4. The factors of production are divisible.
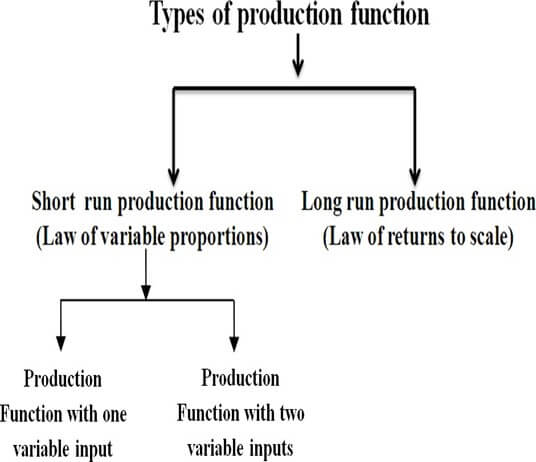
  5. Production function can be fitted to a short run or to long run.
    production function
    production function