Shortest Path Routing
The shortest path algorithm is a fundamental technique used in routing to compute optimal paths within a network. This algorithm is particularly useful when a complete representation of the network is available, allowing for efficient routing decisions even when not all routers have full knowledge of the network’s topology.
Graph Representation of the Network
To implement the shortest path algorithm, the network is modeled as a graph. In this graph, each node represents a router, while each edge represents a communication link between routers. The goal of the algorithm is to find the shortest path between a specified pair of routers by analyzing the graph
Metrics for Path Length
The concept of “shortest path” can be defined using various metrics. The most straightforward metric is the number of hops between routers. For example, in a given network, two paths, ABC and ABE, may have the same number of hops. However, other metrics can also be employed, such as geographic distance (in kilometers) or mean delay of packets. By using different metrics, the algorithm can determine the “shortest” path based on the specific criteria relevant to the network’s performance.
Dijkstra's Algorithm
One of the most well-known algorithms for finding the shortest path in a graph is Dijkstra’s algorithm, introduced by Edsger W. Dijkstra in 1959. This algorithm computes the shortest paths from a source node to all other nodes in the network. The algorithm operates by labeling each node with its distance from the source node along the best-known path. Initially, all nodes are labeled with infinity, indicating that no paths are known. As the algorithm progresses, these labels are updated to reflect shorter paths as they are discovered.
The algorithm works as follows:
1.Initialization: Start by marking the source node as permanent (indicating that the shortest path to this node is known) and label it with a distance of zero. All other nodes are labeled with infinity.
2.Exploration: Examine each node adjacent to the current working node (initially the source node). For each adjacent node, if the sum of the current node’s label and the edge weight to the adjacent node is less than the adjacent node’s current label, update the label with the new shorter distance.
3.Selection of Next Node: After examining all adjacent nodes, select the tentatively labeled node with the smallest label and mark it as permanent. This node becomes the new working node.
4.Iteration: Repeat the exploration and selection process until all nodes have been marked permanent.
Example of the Algorithm
To illustrate Dijkstra’s algorithm, consider the weighted undirected graph shown in the below figure. The weights on the edges could represent distances or delays. The algorithm starts at node A and marks it as permanent. It then examines all adjacent nodes (B, C, and F) and updates their labels based on the distance from A. The process continues, with the algorithm selecting the next node with the smallest label and updating the labels of its adjacent nodes until the shortest path to the target node (D) is determined.
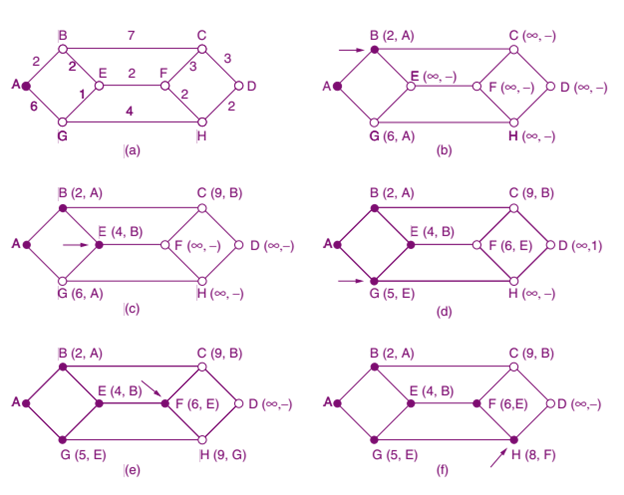
Why the Algorithm Works
Dijkstra’s algorithm is effective because it guarantees that once a node’s label is made permanent, the shortest path to that node has been found. This is due to the nature of the algorithm, which always explores the shortest known paths first. If a shorter path were to exist, it would have been discovered during the exploration of the adjacent nodes.
Implementation Considerations
The implementation of Dijkstra’s algorithm can vary, but it typically involves maintaining a priority queue to efficiently select the next node with the smallest label. The algorithm can be adapted to work in reverse, starting from the target node and labeling nodes with their predecessors, ultimately reconstructing the shortest path in the correct order.
In summary, the shortest path algorithm, particularly Dijkstra’s algorithm, is a powerful tool for routing in networks. By leveraging graph theory and various metrics, it enables efficient and optimal routing decisions that enhance network performance. The flexibility in defining path length metrics allows the algorithm to be tailored to specific network requirements, whether prioritizing speed, distance, or other factors. As networks grow in complexity, the importance of efficient routing algorithms like Dijkstra’s becomes increasingly critical for maintaining optimal communication and resource utilization.
