Error Detection and Correction
In the realm of data communication, ensuring the integrity of transmitted information is paramount. Communication channels exhibit a wide range of characteristics, with some, like optical fiber, having minimal error rates, while others, particularly wireless links and aging local loops, experience significantly higher error rates. As transmission errors are inevitable, especially in less reliable channels, it is crucial to implement effective strategies for error detection and correction.
Understanding Transmission Errors
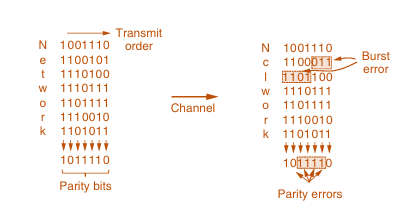
Transmission errors can occur due to various factors, including noise, interference, and physical degradation of the communication medium. These errors can manifest as single-bit errors, where one bit is altered, or as burst errors, where multiple bits are affected in a sequence. To address these challenges, network designers have developed two primary strategies for managing errors:
1.Error-Correcting Codes (FEC): These codes add sufficient redundant information to allow the receiver to deduce the original transmitted data, even in the presence of errors.
2.Error-Detecting Codes: These codes include just enough redundancy to identify that an error has occurred, prompting the receiver to request a retransmission of the data.
Both strategies rely on the addition of redundant information to the data being transmitted, but they serve different purposes based on the reliability of the communication channel.
Types of Errors and Their Models
Understanding the types of errors that can occur is essential for designing effective error detection and correction mechanisms. Errors can be categorized into two primary models:
→ Isolated Single-Bit Errors: These occur sporadically and are often caused by brief spikes in thermal noise.
→ Burst Errors: These happen in clusters, where a sequence of bits is affected, often due to prolonged interference or signal degradation.
The choice of error-correcting or error-detecting codes depends on the expected error patterns. For instance, burst errors are more challenging to correct than isolated errors, but they can be managed effectively with the right coding techniques.
Error-Correcting Codes
Error-correcting codes are designed to enable the receiver to reconstruct the original data even when errors occur. Here are four common types of error-correcting codes:
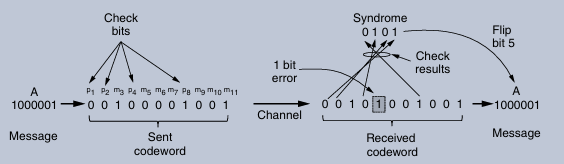
1.Hamming Codes: These codes can correct single-bit errors and detect double-bit errors by adding check bits at specific positions in the data stream.
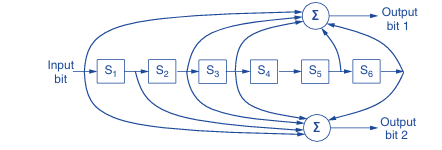
2.Binary Convolutional Codes: Unlike block codes, convolutional codes process a continuous stream of data, using previous bits to influence the current output. They are widely used in applications like GSM and satellite communications.
3.Reed-Solomon Codes: These linear block codes operate on symbols rather than individual bits, making them particularly effective for correcting burst errors. They are commonly used in CDs, DVDs, and data transmission over noisy channels.
4.Low-Density Parity Check (LDPC) Codes: These codes utilize a sparse matrix representation, allowing for efficient decoding and strong error correction capabilities. They are increasingly adopted in modern networking standards.
Error-Detecting Codes
While error-correcting codes are essential for noisy channels, error-detecting codes are often more efficient in high-quality environments, such as fiber optics. Here are three widely used error-detecting codes:
1.Parity Bits: A simple method that adds a single bit to ensure that the total number of 1s in the data is even (or odd). While effective for detecting single-bit errors, it is less reliable for burst errors.
2.Checksums: These involve summing groups of data bits and appending the result as a check value. Checksums are commonly used in network protocols, such as the Internet Protocol (IP).
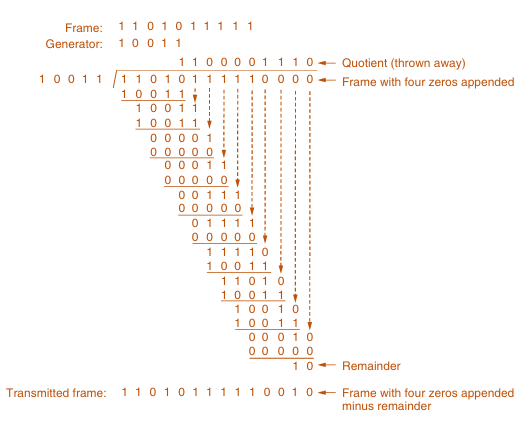
3.Cyclic Redundancy Checks (CRCs): A more robust method that treats data as polynomials and uses polynomial division to detect errors. CRCs are widely used in various networking standards, including Ethernet and Wi-Fi.
Conclusion
Error detection and correction are critical components of reliable data communication. By understanding the types of errors that can occur and implementing appropriate coding strategies, network designers can ensure the integrity of transmitted data. Whether through error-correcting codes like Hamming and Reed-Solomon or error-detecting codes like checksums and CRCs, the goal remains the same: to maintain the accuracy and reliability of data transmission in an increasingly complex communication landscape.