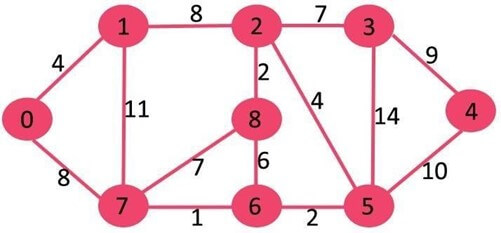
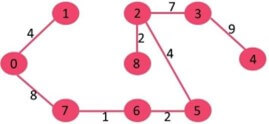
AIM: Implement broadcast tree for a given subnet of hosts

THEORY:

Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.

The steps for finding MST using Kruskal’s algorithm

Sort all the edges in non-decreasing order of their weight.
Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so If cycle is not formed, include this edge. Else, discard it.
Repeat step#2 until there are (V-1) edges in the spanning

The steps for finding MST using Kruskal’s algorithm

Sort all the edges in non-decreasing order of their weight.
Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so If cycle is not formed, include this edge. Else, discard it.
Repeat step#2 until there are (V-1) edges in the spanning tree

Now pick all edges one by one from sorted list of edges

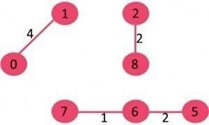
Pick edge 7-6: No cycle is formed, include
Pick edge 8-2: No cycle is formed, include
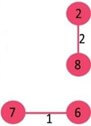
Pick edge 6-5: No cycle is formed, include
Pick edge 0-1: No cycle is formed, include
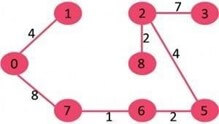
Pick edge 2-5: No cycle is formed, include
Pick edge 8-6: Since including this edge results in cycle, discard
Pick edge 2-3: No cycle is formed, include
Pick edge 7-8: Since including this edge results in cycle, discard
Pick edge 0-7: No cycle is formed, include
Pick edge 1-2: Since including this edge results in cycle, discard
Pick edge 3-4: No cycle is formed, include

ALGORITHM

step 1: declare variable as int p,q,u,v,n;

step 2: Initialize min=99,mincost=0;

step 3: declare variable as int t[50][2],i,j;

step 4: declare variable as int parent[50],edge[50][50];

step 5: Begin

step 6: write “Enter the number of nodes” step 7: read “n”

step 8: Initialize i=0

step 9: repeat step(10-12) until i<n step10: increment i

step11: write”65+i”

step12: Initialize parent[i]=-1

step13:wite “\n”

step14: Initialize i=0

step15: repeat step(15-21) until i<n

step16: increment i

step17: write”65+i”

step18: Initialize j=0 step19: repeat until j<n step20: increment j

step21: read edge[i][j]

step22: Initialize i=0

step23: repeat step(23-43) until i<n

step24: increment i

step25: Initialize j=0 step26: repeat until j<n step27: increment j

step28: if’edge[i]j]!=99

step29: if’min>edge[i][j] repeat step (29-32) step30: intialize min=edge[i][j]

step31: intialize u=i

step32: intialize v=j

step33: calling function p=find(u);

step34: calling function q=find(v);

step35: if’P!=q repeat steps(35-39)

step36: intialize t[i][0]=u

step37: intialize t[i][1]=v

step38: initialize mincost=mincost+edge[u][v]

step39: call function sunion(p,q)

step40: else repeat steps(40-42)

step41: Intialize t[i][0]=-1;

step42: Intialize t[i][1]=-1;

step43: intialize min=99;

step44; write”Minimum cost is %d\n Minimum spanning tree is”,mincost

step45: Initialize i=0

step46: repeat until i<n

step47: increment i

step48: if’t[i][0]!=-1 && t[i][1]!=-1’repeat step(48-50)

step49: write “%c %c %d”, 65+t[i][0], 65+t[i][1], edge[t[i][0]][t[i][1]]

step50: write”\n”

step51: end

step52: called function sunion(int l,int m) repeat step(51-52)

step53: intialize parent[l]=m

step54: called function find(int l) repeat step(53-56)

step55: if parent([l]>0)

step56: initialize l=parent

step57: return l

Program:

#include<stdio.h>

int p,q,u,v,n;

int min=99,mincost=0;

int t[50][2],i,j;

int parent[50],edge[50][50];

main()

{

printf(“\n Enter the number of nodes”);

scanf(“%d”,&n);

for(i=0;i<n;i++)

{

printf(“%c\t”,65+i);

parent[i]=-1;

}

printf(“\n”);

for(i=0;i<n;i++)

{

printf(“%c”,65+i);

for(j=0;j<n;j++)

scanf(“%d”,&edge[i][j]);

}

for(i=0;i<n;i++)

{

for(j=0;j<n;j++)

if(edge[i][j]!=99)

if(min>edge[i][j])

{

min=edge[i][j]; u=i;

v=j;

}

p=find(u);

q=find(v);

if(p!=q)

{

t[i][0]=u;

t[i][1]=v;

mincost=mincost+edge[u][v];

sunion(p,q);

}

else

{

t[i][0]=-1;

t[i][1]=-1;

}

min=99;

}

printf(“Minimum cost is %d\n Minimum spanning tree is\n”

,mincost); for(i=0;i<n;i++)

if(t[i][0]!=-1 && t[i][1]!=-1)

{

printf(“%c %c %d”, 65+t[i][0], 65+t[i][1], edge[t[i][0]][t[i][1]]);

printf(“\n”);

}

sunion(int l,int m)

{

parent[l]=m;

}

find(int l)

{

if(parent[l]>0) l=parent[l];

return l;

}

Output:

Enter the number of nodes 4

	A	B	C	D
A	1	3	5	6
B	6	7	8	9
C	2	3	5	6
D	1	2	3	7

Minimum cost is 9 Minimum spanning tree is

B A 6

C A 2

D A 1