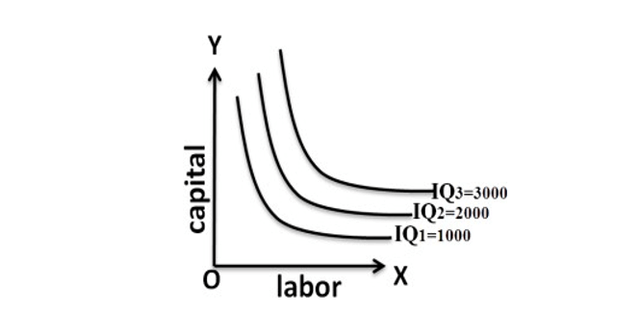
Production Function With Two Variable Inputs

Isoquants analyse and compare the different combinations of capital & labour and output. The term isoquant has its origin from two words “iso” and “quantus”. „iso‟ is a Greek word meaning „equal‟ and „quantus‟ is a Latin word meaning „quantity‟. Isoquant therefore, means equal quantity. An isoquant curve is therefore called as iso-product curve or equal product curve or production indifference curve.

Thus, an isoquant shows all possible combinations of two inputs, which are capable of producing equal or a given level of output. Since each combination yields same output, the producer becomes indifferent towards these combinations.

Assumptions:

1. There are only two factors of production, viz. labour and capital.
2. The two factors can substitute each other up to certain limit
3. The shape of the isoquant depends upon the extent of substitutability of the two inputs.
4. The technology is given over a period.

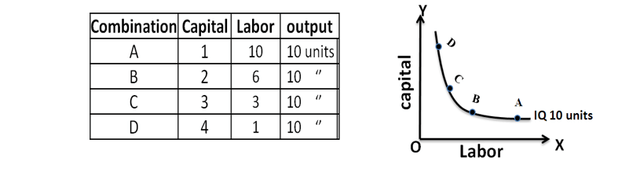
For example:- Now the firm can combine labor and capital in different proportions and can maintain specified level of output say, 10 units of output of a product X. It may combine alternatively as follows: In the below table, combination „A‟ represent 1 unit of capital and 10 units of labour and produces „10‟ units of a product. All other combinations in the table are assumed to yield the same given output of a product say „10‟ units by employing any one of the alternative combinations of the two factors labour and capital. If we plot all these combinations on a paper and join them, we will get a curve called Iso-quant curve as shown below.

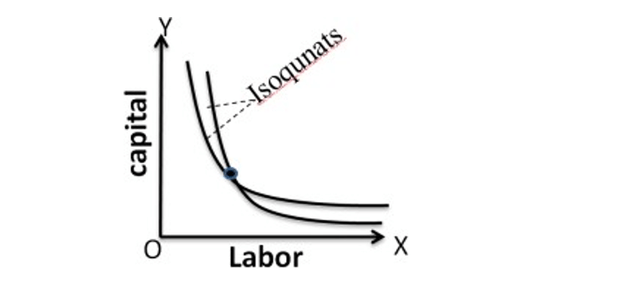
Labour is on the X-axis and capital is on the Y-axis. IQ is the Iso-Quant curve which shows all the alternative combinations A, B, C, D which can produce 10 units of a product.

Features of an ISOQUANT:

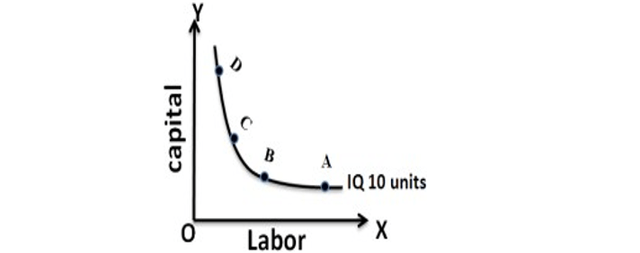
1. 1. Downward sloping: If one of the inputs is reduced, the other input has to be increased. There is no question of increase in both the inputs to yield a given output.

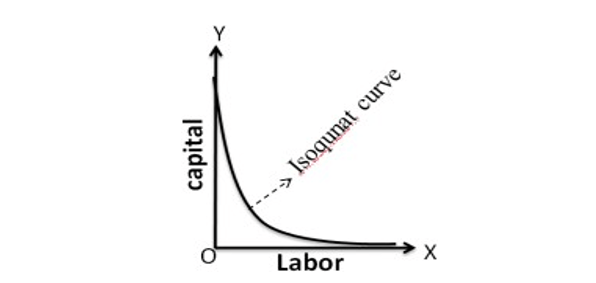
1. 1. Don’t touch the axes: The isoquant touches neither X-axis nor Y-axis, as both inputs are required to produce a given product. If an isoquant is touching the X-axis, it means output is possible even by using a factor(Ex: Labor alone without using capital). But, this is unrealistic.

   2. 

1. 1. Don’t intersect: Iso-quants representing different levels of output never intersect or touch or be tangent to each other. If they intersect to each other, they have a common point on them which means that the same amount of labor and capital produce two different levels of output.

      

1. 1. Convex to origin: Isoquants are convex to the origin. It is because the inputs factor are not perfect substitutes. One input factor is substituted by other input factor in a decreasing marginal rate. The convexity of isoquant suggests that MRTS is diminishing which means that as quantities of one factor-labor is increased, the less of another factor-capital will be given up, if output level is to be kept constant.

1. 1. Upper isoquants represent higher level of output: Each isoquant represents a different quantity of output. Higher isoquants indicate a higher level of output.